tarcieri · January 18, 2023 01:08 · Jan 18, 2023 · Mar 3, 2015 · Mar 3, 2015 · Mar 3, 2015
diff --git a/semiprivate.md b/semiprivate.md
@@ -1,5 +1,12 @@
 # Semiprivate Keys
 
+## 🚨 DANGER: INSECURE! 🚨
+
+This may have seemed like a great idea in 2013, but the repeated "set/clear bits", a.k.a. clamping phases at each level of the hierarchy slowly subtract key strength.
+
+Don't use this as described. Check out [Ristretto](https://ristretto.group/).
+
+## Original text
 Semi-private keys are an expansion of the traditional idea
 of asymmetric keys, which have a public/private keypair, to N keys which
 can each represent a different capability level. In the degenerate case,

diff --git a/semiprivate.md b/semiprivate.md
@@ -57,6 +57,6 @@ assert(R == z*P)
 
 ## Credits
 
-Semiprivate keys were originally Zooko's idea. The basic idea is described in [section 6.1 of the Tahoe-LAFS paper](https://gnunet.org/sites/default/files/lafs.pdf)
+Semiprivate keys were originally Zooko's idea. The basic idea is described in [section 6.1 of the Tahoe-LAFS paper](https://gnunet.org/sites/default/files/lafs.pdf).
 
 SAGE code courtesy Samuel Neves
diff --git a/semiprivate.md b/semiprivate.md
@@ -57,6 +57,6 @@ assert(R == z*P)
 
 ## Credits
 
-As far as I know, semiprivate keys were originally Zooko's idea, although I haven't confirmed that with him. The basic idea is described in [section 6.1 of the Tahoe-LAFS paper](https://gnunet.org/sites/default/files/lafs.pdf)
+Semiprivate keys were originally Zooko's idea. The basic idea is described in [section 6.1 of the Tahoe-LAFS paper](https://gnunet.org/sites/default/files/lafs.pdf)
 
 SAGE code courtesy Samuel Neves
diff --git a/semiprivate.md b/semiprivate.md
@@ -57,6 +57,6 @@ assert(R == z*P)
 
 ## Credits
 
-As far as I know, semiprivate keys were originally Zooko's idea, although I haven't confirmed that with him.
+As far as I know, semiprivate keys were originally Zooko's idea, although I haven't confirmed that with him. The basic idea is described in [section 6.1 of the Tahoe-LAFS paper](https://gnunet.org/sites/default/files/lafs.pdf)
 
 SAGE code courtesy Samuel Neves
diff --git a/semiprivate.md b/semiprivate.md
@@ -55,10 +55,6 @@ assert(R == z*P)
 
 ![Ed25519](https://raw.github.com/cryptosphere/rbnacl/master/images/ed25519.png)
 
-## What are the security properties of this system?
-
-o_O
-
 ## Credits
 
 As far as I know, semiprivate keys were originally Zooko's idea, although I haven't confirmed that with him.

diff --git a/semiprivate.md b/semiprivate.md
@@ -57,4 +57,10 @@ assert(R == z*P)
 
 ## What are the security properties of this system?
 
-o_O
+o_O
+
+## Credits
+
+As far as I know, semiprivate keys were originally Zooko's idea, although I haven't confirmed that with him.
+
+SAGE code courtesy Samuel Neves
diff --git a/semiprivate.md b/semiprivate.md
@@ -49,7 +49,7 @@ assert(R == z*P)
 
 ### Figure 1: Semiprivate Key Generation
 
-![NaCl Semiprivate Keys](http://i.imgur.com/VwYGDyJ.png)
+![NaCl Semiprivate Keys](https://i.imgur.com/L6VfXpB.png)
 
 ### Figure 2: Ed25519 (unmodified)
 

diff --git a/semiprivate.md b/semiprivate.md
@@ -57,6 +57,4 @@ assert(R == z*P)
 
 ## What are the security properties of this system?
 
-CodesInChaos says:
-
-"In when you implement your semi-private key scheme, don't forget to add test vectors for scalars with unset bit 254. some implementations of Curve25519 might malfunction in that case"
+o_O
diff --git a/semiprivate.md b/semiprivate.md
@@ -57,4 +57,6 @@ assert(R == z*P)
 
 ## What are the security properties of this system?
 
-o_O
+CodesInChaos says:
+
+"In when you implement your semi-private key scheme, don't forget to add test vectors for scalars with unset bit 254. some implementations of Curve25519 might malfunction in that case"
diff --git a/semiprivate.md b/semiprivate.md
@@ -47,10 +47,14 @@ Test:
 assert(R == z*P)
 ```
 
-### Figure 1
+### Figure 1: Semiprivate Key Generation
 
 ![NaCl Semiprivate Keys](http://i.imgur.com/VwYGDyJ.png)
 
+### Figure 2: Ed25519 (unmodified)
+
+![Ed25519](https://raw.github.com/cryptosphere/rbnacl/master/images/ed25519.png)
+
 ## What are the security properties of this system?
 
 o_O
diff --git a/semiprivate.sage b/semiprivate.sage
@@ -6,8 +6,8 @@ P = E.lift_x(9);
 l = P.order();
 
 x = ZZ.random_element(l);
-S = x*P;
-y = int(hashlib.sha512(str(S)).hexdigest(), 16) % l;
+Q = x*P;
+y = int(hashlib.sha512(str(Q)).hexdigest(), 16) % l;
 z = x*y % l;
-R = y*S;
+R = y*Q;
 assert(R == z*P)
diff --git a/semiprivate.sage b/semiprivate.sage
@@ -0,0 +1,13 @@
+import hashlib
+
+p = 2^255 - 19;
+E = EllipticCurve(GF(p), [0,486662,0,1,0]);
+P = E.lift_x(9);
+l = P.order();
+
+x = ZZ.random_element(l);
+S = x*P;
+y = int(hashlib.sha512(str(S)).hexdigest(), 16) % l;
+z = x*y % l;
+R = y*S;
+assert(R == z*P)
diff --git a/semiprivate.md b/semiprivate.md
@@ -26,23 +26,28 @@ implementation is slightly different.
 
 This is, as best I understand it, how to implement it in terms of NaCl:
 
+Constants:
 * P = NaCl base point (standard group element)
 * l = Order(P)
-* x = private scalar (i.e. random number + some bitflipping)
-* s = x*P (semiprivate key)
-* y = H(s) mod l
-* a = x*y mod l (computed Ed25519 private scalar)
-* A = y*s (Ed25519 public key)
+
+Functions:
+* H(): SHA512 truncated to 256-bits + set/clear bits
+
+Variables:
+* k = random Ed25519 seed
+* x = H(k)
+* Q = x*P (semiprivate key)
+* y = H(Q) mod l
+* z = x*y mod l (computed Ed25519 private scalar)
+* R = y*Q (Ed25519 public key)
 
 Test:
 
 ```
-assert(A == a*P)
+assert(R == z*P)
 ```
 
-### Figure 1 (or something)
-
-NOTE: the variable names don't match the above description, which makes everything all the more confusing
+### Figure 1
 
 ![NaCl Semiprivate Keys](http://i.imgur.com/VwYGDyJ.png)
 

diff --git a/semiprivate.md b/semiprivate.md
@@ -44,7 +44,7 @@ assert(A == a*P)
 
 NOTE: the variable names don't match the above description, which makes everything all the more confusing
 
-![NaCl Semiprivate Keys](https://raw.github.com/tarcieri/semiprivate/master/diagram.png)
+![NaCl Semiprivate Keys](http://i.imgur.com/VwYGDyJ.png)
 
 ## What are the security properties of this system?
 

diff --git a/gistfile1.md → semiprivate.md b/gistfile1.md → semiprivate.md
diff --git a/gistfile1.md b/gistfile1.md
@@ -42,6 +42,8 @@ assert(A == a*P)
 
 ### Figure 1 (or something)
 
+NOTE: the variable names don't match the above description, which makes everything all the more confusing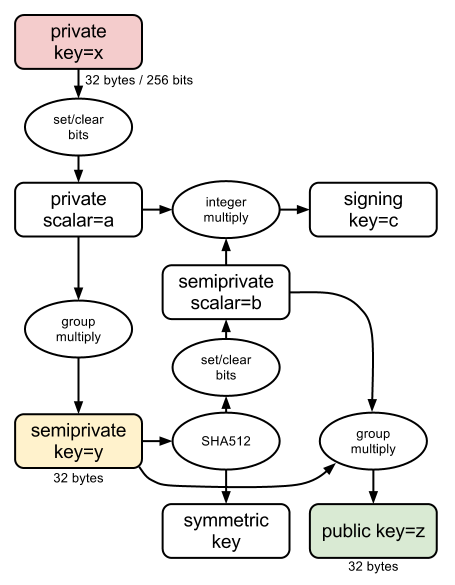
+
 ![NaCl Semiprivate Keys](https://raw.github.com/tarcieri/semiprivate/master/diagram.png)
 
 ## What are the security properties of this system?

diff --git a/gistfile1.md b/gistfile1.md
@@ -26,17 +26,21 @@ implementation is slightly different.
 
 This is, as best I understand it, how to implement it in terms of NaCl:
 
-P = NaCl base point (standard group element)
-l = Order(P)
-x = private scalar (i.e. random number + some bitflipping)
-s = x*P (semiprivate key)
-y = H(s) mod l
-a = x*y mod l (computed Ed25519 private scalar)
-A = y*s (Ed25519 public key)
+* P = NaCl base point (standard group element)
+* l = Order(P)
+* x = private scalar (i.e. random number + some bitflipping)
+* s = x*P (semiprivate key)
+* y = H(s) mod l
+* a = x*y mod l (computed Ed25519 private scalar)
+* A = y*s (Ed25519 public key)
 
+Test:
+
+```
 assert(A == a*P)
+```
 
-Here's a diagram of the system I'm describing, modeled after a similar diagram of Ed25519:
+### Figure 1 (or something)
 
 ![NaCl Semiprivate Keys](https://raw.github.com/tarcieri/semiprivate/master/diagram.png)
 

diff --git a/gistfile1.md b/gistfile1.md
@@ -1,3 +1,5 @@
+# Semiprivate Keys
+
 Semi-private keys are an expansion of the traditional idea
 of asymmetric keys, which have a public/private keypair, to N keys which
 can each represent a different capability level. In the degenerate case,

diff --git a/gistfile1.md b/gistfile1.md
@@ -0,0 +1,43 @@
+Semi-private keys are an expansion of the traditional idea
+of asymmetric keys, which have a public/private keypair, to N keys which
+can each represent a different capability level. In the degenerate case,
+a semi-private key system has 3 different types of keys. These are,
+to use the Tahoe terminology:
+
+* **writecap**: can publish new ciphertexts
+* **readcap**: can read/authenticate ciphertexts
+* **verifycap**: can authenticate ciphertexts
+
+One of the goals of Tahoe is to keep the capability tokens for each
+of these short. Tahoe goes to pretty extreme lengths to do this, like
+symmetrically encrypting an RSA key and storing it along with a file.
+
+I definitely applaud what they've done there and also believe that
+short capabilities are more useful. The real goal of a semi-private
+key system is to produce short capability tokens which are more
+convenient for users to distribute (potentially in non-digital forms)
+
+The problem is Tahoe's description of semi-private keys is intended
+for DSA, however I would like to implement semi-private keys for
+use with NaCl. NaCl uses elliptic curve cryptography, so the
+implementation is slightly different.
+
+This is, as best I understand it, how to implement it in terms of NaCl:
+
+P = NaCl base point (standard group element)
+l = Order(P)
+x = private scalar (i.e. random number + some bitflipping)
+s = x*P (semiprivate key)
+y = H(s) mod l
+a = x*y mod l (computed Ed25519 private scalar)
+A = y*s (Ed25519 public key)
+
+assert(A == a*P)
+
+Here's a diagram of the system I'm describing, modeled after a similar diagram of Ed25519:
+
+![NaCl Semiprivate Keys](https://raw.github.com/tarcieri/semiprivate/master/diagram.png)
+
+## What are the security properties of this system?
+
+o_O
diff --git a/gistfile1.txt b/gistfile1.txt
@@ -1,31 +0,0 @@
-Attempting a little "mathematical prose" here ;)
-
-I'm trying to implement semiprivate keys. These expand the normal idea
-of symmetric keys, which have a public/private keypair, to N keys which
-can each represent a different capability level.
-
-For the purposes of getting started, I'd like to have 3 capability levels:
-one for creating new ciphertexts, one for decrypting and verifying them,
-and one which can only verify but not decrypt. So the goal here is to
-produce keys with 3 capability levels (the degenerate form of semi-private
-keys, as anything lower would be a typical keypair)
-
-I'm trying to implement semi-private keys as defined in the Tahoe paper:
-http://eprint.iacr.org/2012/524.pdf
-
-The problem is Tahoe's description of semi-private keys is intended
-for DSA, however I would like to implement semi-private keys for
-use with NaCl. NaCl uses elliptic curve cryptography, so the
-implementation is slightly different.
-
-This is, as best I understand it, how to implement it in terms of NaCl:
-
-P = NaCl base point (standard group element)
-l = Order(P)
-x = private scalar (i.e. random number + some bitflipping)
-s = x*P (semiprivate key)
-y = H(s) mod l
-a = x*y mod l (computed Ed25519 private scalar)
-A = y*s (Ed25519 public key)
-
-assert(A == a*P)

diff --git a/gistfile1.txt b/gistfile1.txt
@@ -21,11 +21,11 @@ implementation is slightly different.
 This is, as best I understand it, how to implement it in terms of NaCl:
 
 P = NaCl base point (standard group element)
-O = Order(P)
+l = Order(P)
 x = private scalar (i.e. random number + some bitflipping)
 s = x*P (semiprivate key)
-y = H(s) mod O
-a = x*y mod O (computed Ed25519 private scalar)
+y = H(s) mod l
+a = x*y mod l (computed Ed25519 private scalar)
 A = y*s (Ed25519 public key)
 
 assert(A == a*P)
diff --git a/gistfile1.txt b/gistfile1.txt
@@ -6,7 +6,7 @@ can each represent a different capability level.
 
 For the purposes of getting started, I'd like to have 3 capability levels:
 one for creating new ciphertexts, one for decrypting and verifying them,
-and one which can only verify or not decrypt. So the goal here is to
+and one which can only verify but not decrypt. So the goal here is to
 produce keys with 3 capability levels (the degenerate form of semi-private
 keys, as anything lower would be a typical keypair)
 

diff --git a/gistfile1.txt b/gistfile1.txt
@@ -22,7 +22,7 @@ This is, as best I understand it, how to implement it in terms of NaCl:
 
 P = NaCl base point (standard group element)
 O = Order(P)
-x = original private scalar (i.e. random number + some bitflipping)
+x = private scalar (i.e. random number + some bitflipping)
 s = x*P (semiprivate key)
 y = H(s) mod O
 a = x*y mod O (computed Ed25519 private scalar)

diff --git a/gistfile1.txt b/gistfile1.txt
@@ -0,0 +1,31 @@
+Attempting a little "mathematical prose" here ;)
+
+I'm trying to implement semiprivate keys. These expand the normal idea
+of symmetric keys, which have a public/private keypair, to N keys which
+can each represent a different capability level.
+
+For the purposes of getting started, I'd like to have 3 capability levels:
+one for creating new ciphertexts, one for decrypting and verifying them,
+and one which can only verify or not decrypt. So the goal here is to
+produce keys with 3 capability levels (the degenerate form of semi-private
+keys, as anything lower would be a typical keypair)
+
+I'm trying to implement semi-private keys as defined in the Tahoe paper:
+http://eprint.iacr.org/2012/524.pdf
+
+The problem is Tahoe's description of semi-private keys is intended
+for DSA, however I would like to implement semi-private keys for
+use with NaCl. NaCl uses elliptic curve cryptography, so the
+implementation is slightly different.
+
+This is, as best I understand it, how to implement it in terms of NaCl:
+
+P = NaCl base point (standard group element)
+O = Order(P)
+x = original private scalar (i.e. random number + some bitflipping)
+s = x*P (semiprivate key)
+y = H(s) mod O
+a = x*y mod O (computed Ed25519 private scalar)
+A = y*s (Ed25519 public key)
+
+assert(A == a*P)
No results found